🗂️ 문제
링크: https://school.programmers.co.kr/learn/courses/30/lessons/42898#
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
🚀 시행착오
def solution(m, n, puddles): # m: 열, n: 행
answer = 0
dict = {} # key: 경로, value: 경로 개수
visited = [[False] * (m+1) for _ in range(n+1)]
dx = [0, 1] # 아래쪽, 오른쪽
dy = [1, 0]
def DFS(y, x, cnt):
visited[y][x] = True
for ax, ay in zip(dx, dy):
nx = x + ax
ny = y + ay
if m >= nx > 0 and n >= ny > 0:
if not visited[ny][nx] and [nx, ny] not in puddles:
if (nx, ny) == (m, n):
dict[cnt] = dict.get(cnt, 0) + 1
continue
DFS(ny, nx, cnt+1)
visited[ny][nx] = False
DFS(1, 1, cnt=0)
if dict:
min_distance = min(dict.keys())
answer = dict[min_distance] % 1000000007
return answer처음엔 재귀함수 기반 DFS 방식으로 모든 경로를 탐색하고, 학교까지의 거리에 따른 경로의 개수를 딕셔너리에 저장하는 방법을 생각했다.
이때 DFS의 종료 조건은 방문 처리를 수행하는 visited[]에 의존한다. 즉, 모든 노드를 탐색한 경우 함수를 종료하기 때문에, 학교의 좌표인 (4, 3)에 도달했을 때 방문 여부를 False로 지정하여 방문하지 않은 걸로 변경한다. 이로써 2차원의 맵에서 모든 경로를 탐색하여 거리를 구할 수 있다.
위의 방식으로 구한 거리에 따른 경로의 개수 중 최단 거리에 해당하는 개수를 반환하여 구현했다.
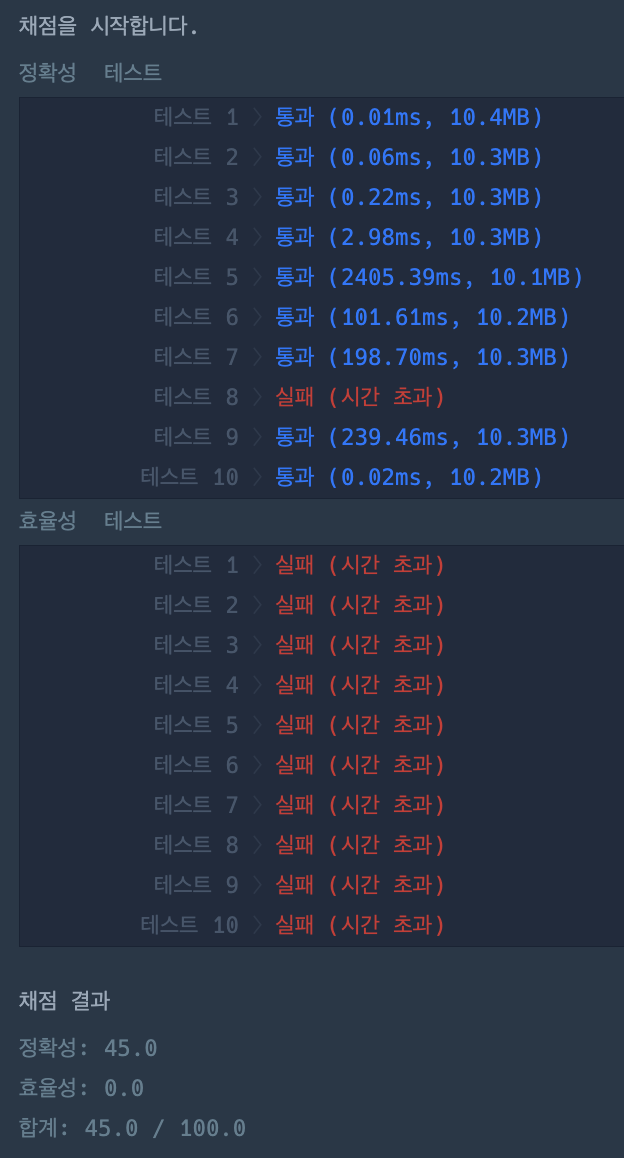
하지만 결과적으로 테스트 케이스는 잘 동작하였으나, 효율성 측면에서 모두 실패했다.
해당 방식의 경우 모든 경로를 탐색해야 하는데 만약 웅덩이 개수= 0, m=10, n=10인 경우, 탐색하는 모든 경우의 수는 벌써 1024가지 경로가 존재하기 때문이다..
💡 접근법
하지만 생각해보니 오른쪽과 아래쪽으로만 움직이기 때문에 어떤 경로로 도착하던간에 항상 최단 경로로 도착하게 된다.
따라서 BFS 방식으로 모든 경로를 탐색하되, 현재 도달한 위치까지의 최단경로의 수를 DP 방식으로 계속해서 업데이트해주면 된다.
(i,j) 위치까지 도달하기 위해선 오른쪽으로 왔을 때 도달한 경우, 아래쪽을 왔을 때 도달한 경우 이 두 가지가 있다. 따라서 (i,j) 위치까지의 최단경로의 수는 (i-1, j) 위치까지의 최단경로 수 + (i, j-1) 위치까지의 최단경로 수로 계산할 수 있다.
이를 점화식으로 나타내면 dp[i][j] = dp[i-1][j] + dp[i][j-1], (i>0, j>0)이다.
😎 내 코드
from collections import deque
def solution(m, n, puddles):
visited = [[False]*(m+1) for _ in range(n+1)]
dp = [[0]*(m+1) for _ in range(n+1)] # m == x
dp[1][1] = 1
dx = [1, 0] # [오른쪽, 아래쪽]
dy = [0, 1]
def BFS(x, y):
queue = deque([(1, 1)])
while queue:
y, x = queue.popleft()
for ax, ay in zip(dx, dy):
nx = x + ax
ny = y + ay
if m >= nx > 0 and n >= ny > 0:
if [nx, ny] not in puddles and not visited[ny][nx]:
queue.append((ny, nx))
visited[ny][nx] = True
if m >= nx-1 > 0 and n >= ny-1 > 0:
dp[ny][nx] = dp[ny][nx-1] + dp[ny-1][nx]
elif m >= nx-1 > 0:
dp[ny][nx] = dp[ny][nx-1]
else:
dp[ny][nx] = dp[ny-1][nx]
BFS(1, 1)
return dp[n][m] % 1000000007
🧐 배운 점
- dict[cnt] = dict.get(cnt, 0) + 1
'Algorithm > Programmers' 카테고리의 다른 글
| [BFS] 프로그래머스 Lv3. 가장 먼 노드 - python (0) | 2025.03.07 |
|---|---|
| [DP] 프로그래머스 Lv3. 정수 삼각형 - Python (1) | 2025.02.06 |
| [정렬] 프로그래머스 Lv2. 가장 큰 수 - Python (2) | 2025.01.31 |
| [스택/큐] 프로그래머스 Lv2. 주식가격 - Python (0) | 2025.01.14 |
| [DFS] 프로그래머스 Lv2. 타겟 넘버 - Python (0) | 2025.01.11 |
